بحث عن الدوال الحقيقية وأنواعها

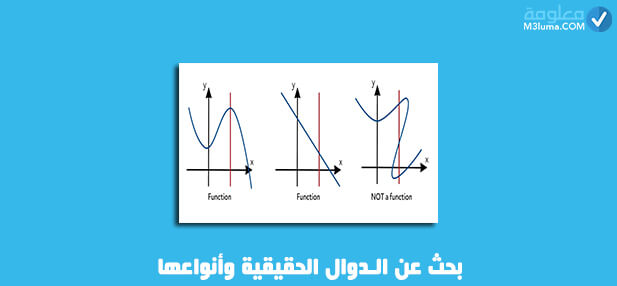
بحث عن الدوال الحقيقية وأنواعها

من بين الدروس التي يدريها الطلبة في الرياضيات والفيزياء هو درس الدوال الذي يجده اغلب الطلاب من الدورس الصعبة، وذلك باختلاف وتعدد انواع هذه الدوال، التي تختلف منحنياتها، حيث هناك كل من دوال مركبة والدوال عكسية وغيرها.

فإذا كنت من الطلاب الذين يرغبون بشرح بسيط ومفهوم حول الدوال وانواعه، فأنصحك بالقراءة هذه المقال إلى النهاية، حيث سنقدم لكم فيها العديد من الفقرات التي تتحدث عن الدالة وأنواعها ومجال الدالة وتغييراتها، وغيرها من الأشياء المهمة، كل ذلك يمكنكم التعرف عليه من خلال هذه المقال، لهذا أنصحكم بتركيز جيدا لفهم كل ذلك هيا بنا:

تعريف الدوال Function

ببساطة الدوال هي تمثيل رياضي لعلاقة بين العديد من العناصر والتي يطلق عليها “المنطق” وأيضا عناصر أخرى يطلق عليها “المستقر”. يتم الرمز للعنصر المرتبط بالمنطق بحرف “X” اما العنصر المرتبط بالمستقبل يرمز له ب حرف “Y”.

من المحتمل أن يرتبط على كم عنصر المنطق والمتسقر معا ولكن بشرط ان لا يكون هذا الارتباط يشمل اكثر من عنصرين، وذلك لتجنب عدم حدوث خلط بين كل من المنطق والمسقر.

من خلال بين كل من المنطق والمتسقر تنتج الدالة، والتي من خلالها يمكن التعرف على القيم التي يتوفر عليها المستقر وذلك نتيجة تحول المنطق لجزئيات في المستقر.

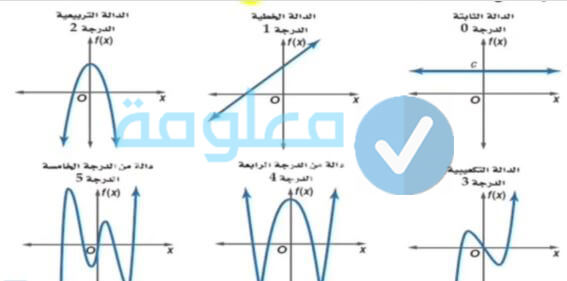
انواع الدوال Type of Functions

تنقسم الدوال إلى مجموعة من الأقسام المختلفة، دعونا نتعرف عليها بالصور في هذه الفقرة من المقال تابعوا معنا الشرح:

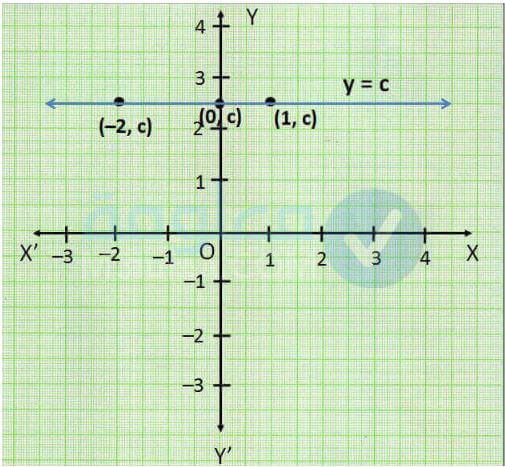
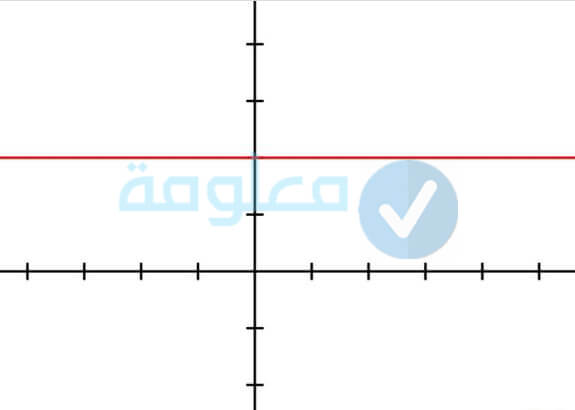
الدالة الثابتة

وهي التي يكون الاقتران بها وتكون قيمة التابع لا تتغير حيث تكون قيمة ثابتة. لا تتغير قيمة الثابت مهما كانت قيمة الوسيط للدول، هذا ما يجعل الدالة الثابتة تتميز عن باقي الدوال الأخرى.

تتوفر الدالة الثابتة على مجموعة من الخصائص، من بينها القيمة التي تساوي صفر إلى جانب أن المتغير التابع يكون ثابت ولا يتغير، ويمكن تمثيل هذه الدالة على شكل الاحداثيات الديكارتية، من خلال الخط المستقيم موازي لمحور السينات والذي يتقاطع مع محور الصادات عند القيمة الثابتة. صيغتها العامة هي f (x)= a.

متعددة الحدود

تعتبر هذه الدالة من بين أكثر الدوال متعددة الحديدة التي تتوفر على اكثر من المتغيرات والمعاملات، والتي يتم بناؤها عن طريق الجمع والطرح او القسمة او الضرب حيث يكن التي صحيحا وليس سالب P(x)=amxn+an–1xn–1+⋯+a1x+a0.

الدالة الجبرية

وهي عبارة عن دالة يمكن إزالة الى منها لاجراء أكثر من عملية واحدة من القسمة والضرب والجمع f(x)=x²+3x+6

الدالة التربيعية

الصبغة العامة الخاصة بالدالة التربيعية هي: f (x) = ax2 + bx + c
تتوفر هذه الدالة على ثلاث متغيرات: z على الحدود x² ; y² ; z² ; xy ; xz ; yz ; x ; y ; z تابث يعني                                         f(x,y,z) = ax² + by² + cz² + dxy² + exz + fyz + gx + iz + j.
الدالة التربيعية أحادية المتغير تكون بإضافة a أو b أو c أو d أو e أو f لكل من للحدود ذات الدرجة الثانية بشرط ان لا يكون أحدهما يساوي 0 وصيغتها على الشكل التالي: f(x,y) + ax² + by² + cxy + dx + ey +f.

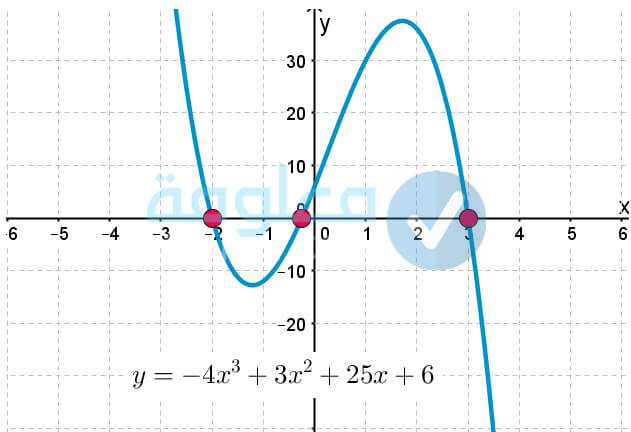
الدالة التكعيبية

الصيغة العامة لهذه الدالة هي:  f (x) = ax3 + bx2 + cx + d

الدالة الكسرية

تتمثل الدالة الكسرية في كل دالة يمكن كتابتها في صورة نسبة بين دالتين متعددتي الحدود.

بحيث (x) P ينتمي المجموعة R و (x) Q يخالف الصفر.

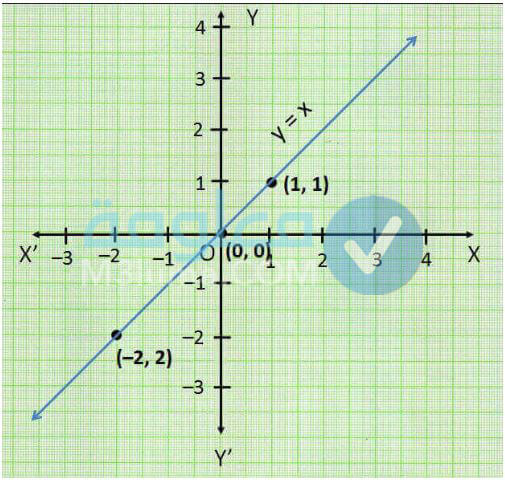
الدالة المحايدة

وهي الدالة التي يطلق عليها f هي دالة متطابقة او محايدة وذلك في حالة كان f (x) = x ، ∀x∈A بحيث f: A → B.

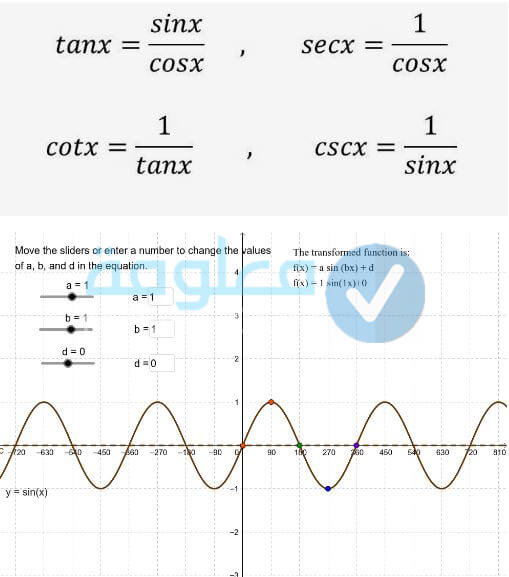
الدوال المثلثية

وهي الدوال التي تعتمد على علاقة حساب المثلثات وهي y=sinx و y = cosx و y = tanx.

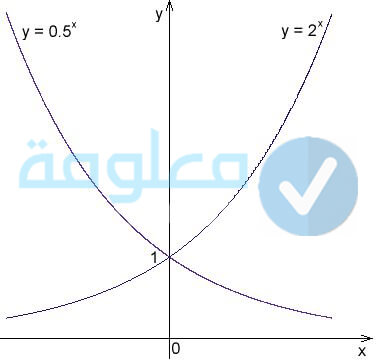
الدوال الاسية

يتم استخدام الدوال الاسية في العديد من العلوم الأخرى لهذا تعتبر احد اكثر الدوال الشائعة، وذلك لانها تعمل على تسهيل اجار عمليات حسابية في كل من الفزياء والكيمياء والهندسة وغيرها من العلوم الأخرى، صيفتها على الشكل التالي f(x)=ax ,a > 0 , a ≠1. وبمعنى ادق الدالة الاسية هي الدالة التي تكون اعدادها متساوية لكنها لا تساوي صفر.

اللوغاريتم

وهي الدالة العكسي للدوال الاسية (f(x)=loga(x على سبيل المثال دالة لوغاريثم 100 بالنسبة الاساس 10 هو 10 × 10 =10².

• الدالة المركبة: وهي الدالة التي يكون الاقتران فيها مركب.
• الدالة التحليلية: وهي الدالة التي تتوفر على العديد من القيم العقدية ومن بين الأمثلة الخاصة بها هي الدوال المثلثية والدوال المتعددة والدوال اللوغاريتمية ودوال الرفع.
• الدالة الضمنية: تعطي هذه الدلالة قيم ودلالاته متغيرة ويكون الاقتران فيها بشكل ضمني.
• الدالة الزوجية: هي الدالة التي يكون فيها الاقتران بشكل زوجي وتتوفر على شريك متعلق بالتماثل.
• الدالة المتطابقة: وهي الدالة التي يكون الاقتران فيها متطابق والتي تكون مرتبطة بعناصرها.
• الدالة العكسية: وهي الدالة التي تنعكس عناصرها على المحال المقابل على سبيل المثال في حالة كانت الدالة تناظرية A إلى b تكون الدالة العكسية إلى b إلى A.
• الدالة الفردية: وهي الدالة التي يشترك فيها التماثل ويكون ليها الاقتران فريدي.
• الدالة التزايدية: هي الدالة التي يكون في الاقتران متزايد على سبيل المثال منها الدالة التكعبية والدالة التربيعية.
• الدالة المستمرة: وهي الدالة التي تتخد شكل رياضي والتي يكون فيها الاقتران بسيط.
• الدالة المتناقضة: وهي الدالة التي يكون فيها الاقتران بشكل متناقض.
• الدالة الصريحة: وهي الدالة التي يكون فيها الاقتران بشكل صريح.
• الدالة الشاملة: وهي الدالة التي يكون فيها التطابق في جميع مجالاتها مع المجال المقابل.

أنواع الدوال المتغيرة وفقاً لعدد المتغيرات

تنقسم الدوال إلى مجموعة من الأشكال وذلك حسب عدد المتغيرات،عونت نتعرف على انواع هذه الدوال المتغيرة وفقاً لعدد المتغيرات:

فإذا كانت الدالة تتوفر على متغير واحد في مجالها عندها تنسى الدالة المتغيرة الواحد المستقل ومن بين الأمثلة التي ترتبط بها هي العلاقة بين الدخل والانفاق.
اما إذا كانت تتوفر على متغيرين إثنين في مجالها عندها تسمى الدالة ذات متغيرين مستقلين ومن الأمثلة المرتبط بها هي مساحة المستطيل.
وفي حالة كانت بثلاثة متغيرات فتسمى عندها بالدالة ذات ثلاثة متغيرات مستقلة ومن الأمثلة المرتبط بها هو متوازي الأضلاع.

انواع الدوال حسب شكلها الرياضي

الدالة الثابتة: وهي الدالة التي تمتاز يتوفر عنصر واحد ويتم التعبير عنها بصيغة التالية:  f(x=c حيث c ∈R.
الدوال كثيرة الحدود: يتم التعبير عن هذه الدالة من خلال كتابة الصيغة التالية: f(x)=an n+ an-1 xn1 + an-2 xn-2+……………+ a0 x0 +a0.

تمثيل الدوال المتغيرة

تنقسم الدول المتغيرة إلى أربعة أقسام، دعونا نتعرف عليها في الأسطر التالية من هذه الفقرة، تابعوا معنا الشرح إلى النهاية:

التمثيل البياني

وهي التي تكون فيها عناصر المنطق تتمثل عل محور “س”. ونتمثل العناصر الخاصة بالمستقر على المحور “ص”. حيث يمثل كل عنصر من صورته في نفس النقطة لنحصل على بعض النقاط التي نقوم بربطها معا، حتى تتكون لدينا الشكل البياني الخاص بالدالة.

التمثيل الجبري

في حالة كان: د(س)=3س+1 فأوجد المصادر 4 ، 5

في الحل هو

د(5)=3(5)+1=16

د(4)=3(4)+1=13

أشكال أخرى للدول المتغيرة

• تمثيل باستخدام نظام القائمة.
• تمثيل كلامي.

تغيرات الدوال المتغيرة

تنقسم التغيرات الخاصة بالدول المتغيرة إلى ثلاثة متغيرات وهي العكسية والمركبة والطردية، دعونا نتعرف عليها بشكل أكبر في الأسطر التالية من هذه الفقرة تابعوا معنا الشرح إلى النهاية:

التغيرات العكسية

وهي التي يكون فيها تغير عكسي يدخل على المتغيرين.

التغيرات المركبة

وهي التي يختلط فيها المتغير الطردي مع المتغير العكسي.

التغيرات الكردية

وهي التي يتغير فيها شكل المتغيرين إلى شكل واحد مع المراعاة ثبات النسبة التي توجد بينهم، على سبيل المثال:
إذا كان المتغيران أ/ب = س إذن النسبة هي أ/ب = س.

أمثلة عن الدوال

في هذه الفقرة سنقدم لكم مجموعة من الأمثلة، حول الدوال التي تحدثنا عنها في الأعلى، مع تقديم صور موضحة لهذه الدوال تابعوا معنا الشرح للتعرف على كل ذلك في الأسطر التالية من هذه المقال تابعوا معنا الشرح:

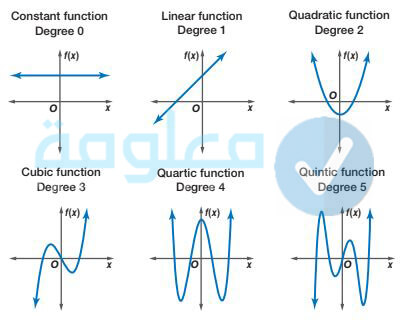
كثيرات الحدود ودوالها

كثيرات الحدود وهي التي تكون الاقترانات الخاصة بها على الشكل التالي: أ_ن س ^ن + أ_ن-1 س ^ن-1 +أ_ن-2 س ^ن-2 +……. أ₀ حيث أ_ن لا يساوي صفر والتي تنتمي إلى الأعداد الطبيعية، تسمى  أ_ن ^، أ_ن-1 ، أ_ن-2 ^، ……. أ₀ حيث يكون المعامل الأول منها هو (f (x) = 0)والذي يعتبر المعامل الرئيسي في الدالة. كما أن جميع المعاملات كثيرات الحدود تكون أصفار بالاقتران الصفري والذي هو (0= (x) f) والذي لا يتوفر على درجة ويمثله المحور x في المحور الديكارتي.

إلى جانب ذلك فإن محال الاقتران الخاص بكثيرات الحدود هو عبارة عن مجموعة من الأعداد الحقيقية، والمدى الخاص به عبارة عن مجموعة من الأعداد الجزئية أو الحقيقية وذلك حسب نوع الاقتران. كما يتم تحديد درجة كثيرات الحدود حسب للأس الأكبر في الدالة، وفي الأسطر التالية من هذه المقال، سنتعرف على انواع الاقترانات كثيرة الحدود، لكن قبل ذلك دعونا نقدم لكم مجموعة من الصور التي تبين التمثيل البياني العام لأنواع مختلفة من كثيرات الحدود، ووجب التذكير ان درجة كثيرة الحدود تصف عدد المقاطع السينية كنا هو موضح في الصورة التالية:

الدال الثابتة

وهي من بين دوال البسيطة من حيث انواع الاقترانات الخاصة بها والحدود، حيث تكون درجة 0 في الحدود الخاصة بها بمعنى أدق ان أي (س) يساوي صفر. وأي رقم مرفوع للقوة صفر تكون النتيجة الخاصة به هي واحد، إذن عندما يضرب بأي رقم فالنتيجة ستكون هي الرقم نفسه، دعونا نقدم لكم مثال تقريبي مع البياني التمثيلي الدالة الثابتة تابعوا معنا الشرح:

f(x) = x⁰ * a
f(x) = 1* a
f (x) = a، حيث إن a هو أي رقم حقيقي.
على سبيل المثال: (f (x) = 3)

الدالة الخطية المتناقصة

تعتبر الدالة الخطية المتناقصة أحد فروع الدالة الخطية، وتم اطلاق هذا الإسم عليها بسبب الخط الذي تتمثل به على الرسم البياني ينحدر للأسفل وذلك كلما زادت قيمة (x). بمعنى صورة الاقتران (x) f تقل مع تزايد الرقم الذي يتم وضعه مكان (x) في كل مرة. عندها يكون معامل (x) سالب ومثال على ذلك (f (x) = -2x + 1) أو (f (x) = -x)

في حالة قمنا بوضع (f (x) = -x) وقمنا بإبراو نتائج تعويض أرقام مختلفة مكان (x) ستظهر لنا النتائج على الشكل الآتي:

• عند تعويض الرقم 1 سيكون الناتج هو -1.
• عند تعويض الرقم 2 سيكون الناتج هو -2.
• عند تعويض الرقم 3 سيكون الناتج هو -3.
• عند تعويض الرقم 4 سيكون الناتج هو -4، وهذا كلما زادت قيمة (x) قلت قيمة f (x).

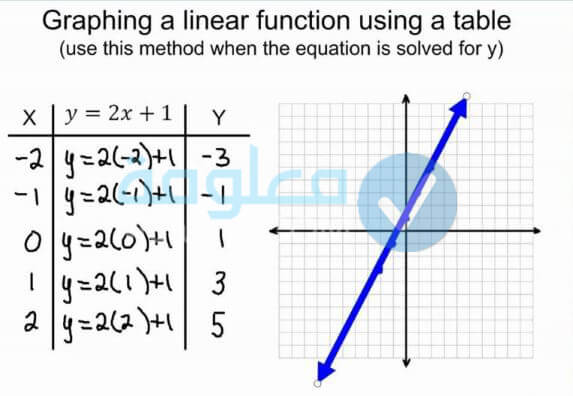
الدالة الخطية

وهي الدالة التي تتوفر على نسبة كبيرة من الدال الثابتة، حيث يكون فيها رأس المتغير (س) هو واحد. وأما صيغتها العامة فيتم التعبير عنها بشكل التالي:  (f (x) =ax +c) دعونا نتعرف على توضيح لهذه الصيغة اكثر:

f(x) = ax¹ + c ، x¹ = x ،
وبالتالي: f(x) = ax + c

والطريقة التي يمكنكم الاعتماد عليها لرسم الدالة الخطية وهي عن طريق وضع نقطتين تمثلان أي رقمين حقيقين والتمثيل بينهما. للحصول على نتيجة واضحة ودقيقة يمكن وضع 5 نقاط اثنان منها في السالب واثنان في الموجب ونقطة واحدة في الصفر، عندها يجب تعويض هما في الاقتران، ووضع النقاط في الرسم البياني على الشكل ( س . ص ) بمعنى ان كل رقم تم تعويضه مع إجابته ثم التوصيل بين النقاط، شاهد الصورة التي توجد في الاسفل للتوضيح أكثر.

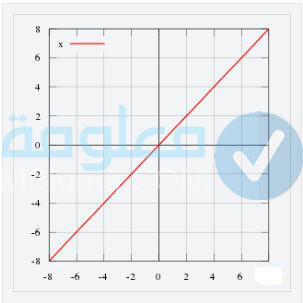
الدالة المحايدة

تعتبر الدالة المحايدة هي الأخرى أحد الدوال التابعة للدالة الخطية، والتي تكون قيمة (x) مساوية مع قيمة ((x) f وذلك عند التعويض والتمثيل البياني، ويتم التعبير عن هذه الدالة من خلال الصيغة التالية: f (x) = x) والسبب في تسمية الدالة المحايدة بهذا الإسم يرجع إلى القيمة المتغيرة وصورته المتساوية وواحد بشكل دائم، حيث تكون فيها نتائح تعويض الأرقام على الشكل الآتي:

• عند تعويض الرقم 1 سيكون الناتج هو 1.
• عند تعويض الرقم 2 سيكون الناتج هو 2.
• عند تعويض الرقم 3 سيكون الناتج هو 3.
• عند تعويض الرقم 4 سيكون الناتج هو 4، أي أن قيمة (x) مساوية لقيمة (f (x) دائمًا.

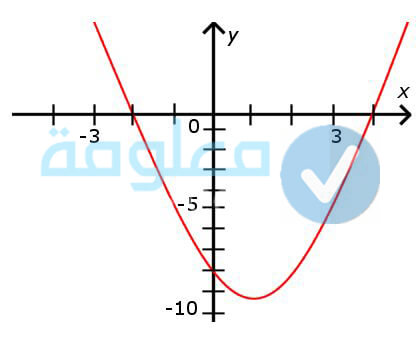
الدالة التربيعية

من بين أشكال متغيرات الحدود الدالة التربيعية، والتي يكون فيها الاقتران هو الثاني بمعنى انه يكون فيها المتغير الأساسي مرفوع للقوة 2 وصورة التي يتم التعبير بها عن هذه الدالة هي (f(x) = ax² +bx + c) حيث يقطع هذا التمثيل منحنى السينات مرتان، ومن خلالايحاد ثلاث نقاط يتم رسم التمثيل البياني الخاص به بكل بساطة، حيث تم ن النقطة الأولى الثانية هم أصغر الاقتران الثالثة هي قمة المنحنى، والتي يطلق عليها اسم صور رأس القطع التي ينقسم عنها المنحنى إلى نصفين متماثلين. دعونا في الأسطر التالية من هذه المقال نتعرف 7دعلى بعض الأمثلة لرسم المحنى التعبيري بالخطوات:

نأخد على سبيل المثال: (f(x) = x² – 1)

يتوفر على مقاطعات سينيان يتم ايجادهما على الشكل التالي:

نضع رقم صفر مكان (x) f ليصبح الاقتران على صورة معادة كا هو موضح في المثال التالي: x² -1 = 0
ولحل المعادلة يتم نقل رقم 1 الى الجهة الأخرى من المعادلة، وبعدها وضع جذر للطرفين على الشكل التالي:

x² = 1 ومن خلال وضع الجذر التربيعي للطرفين نحصل على نتيجة التالية:
x = 1 و x = -1
ويمكن حلها أيضا عن طريق تحليل فرق بين مربعين كما هو موضح في مثال التالي:

0 = x² – 1
0 = (x – 1) (x + 1)
1 – = x و 1 = x

رأس القطع: وهي النقطة الثالثة والتي يمكن العثور عليها عن طريق التعويض في (b/ 2*a-) ليكون الناتج على الشكل التالي:
( b/ 2*a-) = (0/ 2*1-) = 0  أي أن الحد الاوسط غير موجود وبالتالي (b=0) فتكون قيمة رأس القطع في كل الحالات التي لا تتوفر على حد أوسط مع الاقتران التربيعي هي صفر، وليس هناك أي حاجة التعويض في هذه الحالة
صورة رأس القطع هي: (f(x) = 0² – 1)
f(x) =-1

لنحصل بذلك على ثلاث نقاط وهي الحسينيات ورأس القطع وعلى التوالي: (0,1)، (-0,1)، (1,0-) ونقوم بتعويضها على المحور الديكارتي لنحصل بذلك على التمثيل البياني، وهو الذي يتمثل في الرسمة اليمنى العليا كما في الصورة التي توجد في الاسفل والمحدد عليها اللون الأخضر، وهو الذي يمثل مجموعة من التمثيلات البيانية الاقترانات متعددة يمكنك الاستفادة منها.

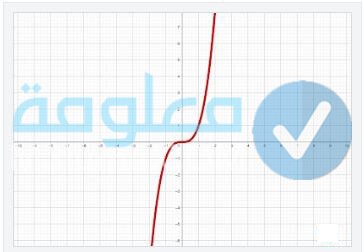
الدالة التكعيبية

الدالة التكعيبية هي من بين الدوال المتفرعة كم كثيرات الحدود كما هناك بعض الدول الأكثر منها، لكن دعونا في هذه الفقرة نتحدث فقط عن الدالة الدالة التكعيبية، التي تكون درجة الاقتران فيها هي الثالثة تبعا للأس، حيث يكون أكبر (x) فيها مرفوع للأس 3، واما الصورة القياسية الخاص بها يتم التعبير عنها على الشكل التالي: (f(x) = ax³ +bx² + cx+ d).

يكون الاقتران في هذه الدالة بثلاثة مقاطع سينية، والتي يمكن تمثيلها عن طريق تعويض مجموعة من القيم مع الاقتران. لكن للحصول على نتيجة دقيقة اكثر يمكن تمثيلها عن طريق برنامج الاكسل او بعض التطبيقات الخاصة بالرسم. حيث يعتبر الدالة التكعيبية عبارة عن رسم صعب رسمه من خلال اليد، وذلك ما سيظهر لكم من خلال التمثيل البياني الذي سنعرضه عليكم في الاسفل والخاص بالاقتران التكعيبي.

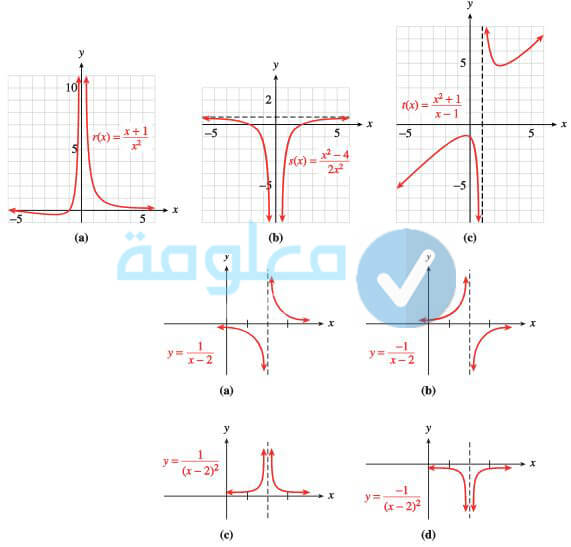
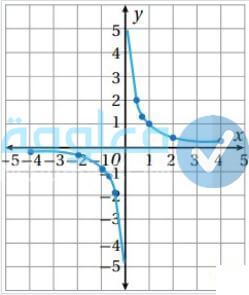
الدالة النسبية

من دوال الجديدة وهي الدالة النسبية، والتي يمكن كتاب الاقتران الخاص بها بصور نسبية كثيري الحدود د، مثل (f (x) /g (x)، بشرط ان (x)g لا يكون مساوي الصفر، كما ان مجال الاقتران النسبي هو عبارة عن مجموعة من الأعداد الحقيقية، هذا الذي يجعل المقاوم مساوي للصفر. وللعثور على المجال يجب تحليل العديد من الحدود الموجودة في المقام من اجل إيجاد الأصفار، دعونا نتعرف على مثال عن محال الاقتران النسبي في الأسطر التالية من هذه الفقرة:

المثال: : (f(x) = (x + 2)/(x² – 9

للعثور على مجال الاقتران النسبي يحب تحليل الكثير من الحدود التي تتواجد في المقام عن طريق تحويل الاقتران إلى معلمة من خلال وضع رقم 0 مكان (x) f على شكل التالي: 0 = x² – 9، عندها تكون هناك طريقتين لكل المعادلة دعونا نتعرف عليهما في الأسطر التالية:.

يجب

• نقل الرقم (9) إلى الجهة الأخرى من المعادلة، وبعدها نضع الجذر التربيعي للطرفين كما يأتي:
  9 = x² ، ثم نضع جذرًا تربيعيًا للطرفين ونحصل على:
  3 – = x و 3 = x

وتحليل فرق بين مربعين على الشكل التالي:
0 = x² – 9
0 = (x – 3) (x + 3)
3 – = x و 3 = x ،

من خلال طريقتين السابقين يتم الحصول على نفس النتيجة، بمعنى أن اصفار المقام هما {3, -3} فيكون المجال هو ح – {3, -3}.

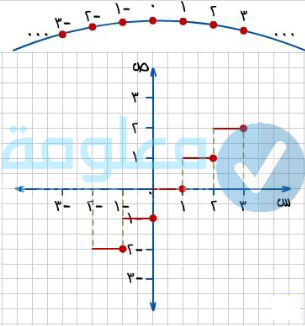
الدالة الدرجية (اقتران أكبر عدد صحيح)

الدالة الدرجية هي من بين الدوال الحقيقية، والتي يكون الاقتران f فيها يقترن مع كل عدد صحيح حقيقي أقل من او يساوي x يتم الرمز إليه ب [x] حيث إذا كان n≤x<n+1 حيث ان n عدد صحيح فإن f(x) = [x] = n

سنصحل على النتائج التالية عند تعويض قيم متعددة في الاقتران f(x) = [x]:

• عند تعويض الرقم -1 سيكون الناتج هو -1.
• عند تعويض الرقم 4 سيكون الناتج هو 4.
• عند تعويض الرقم 1.8 سيكون الناتج هو 1.
• عند تعويض الرقم -2.5 سيكون الناتج هو -3.

وهذا هو التمثيل البياني الخاص به:

الدالة الاسية

والتي تكون على الشكل الصيغة التالية  f(x) = a * b^g(x) +c، حيث أن (x)g يكون اقتران حقيقي وباقي الرموز التالية a و b و C تكون جمعها أعداد حقيقة، حيث ان a لا تساوي صفر، و b اكبر من صفر، وان (x)g يسمى رأس، ورمز b يكون هو الاساس في الاقتران، دعونا نقدم لكم في الاسفل رسم يمثل الاقتران الأسي f(x) = a^x تابعوا معنا الشرح:

يتم تعويض مجموعة من القيم لرسم الاقتران  f(x) = 2^x على الشكل التالي:

• عند تعويض الرقم -2 سيكون الناتج هو (1/4). فتتكون النقطة (-2، 1/4).
• عند تعويض الرقم -1 سيكون الناتج هو (1/2). فتتكون النقطة (-1، 1/2).
• عند تعويض الرقم 0 سيكون الناتج هو 1. فتتكون النقطة (0، 1).
• عند تعويض الرقم 1 سيكون الناتج هو 2. فتتكون النقطة (1، 2) 1.
• عند تعويض الرقم 2 سيكون الناتج هو 4. فتتكون النقطة (2، 4).

وبعدها يتم رسم المستوى الإحداثي ويتم وضع عليه النقاط التي تم إيجادها مسبقا، لنصل بينها بخط وتظهر على الشكل التالي:

الدالة اللوغاريتمية

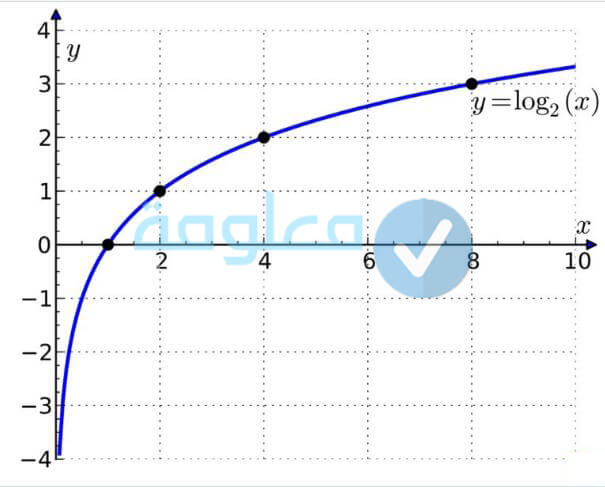
في حالة كانت س> صفر، أ> صفر، أ لا يساوي 1، فإن f(x) =log_a (x)، وذلك إذا وفقط إذا كانت x = a^f(x)، يتم تعريف هذا الاقتران بالقاعدة التالية log_a (x)= f(x) هو الاقتران الذي يطلق عليه اسم الاقتران اللوغاريتمية حيث ان a هو أساس اللوغاريتم، دعونا نعرف لكم العديد العديد من التطبيقات اللوغاريتمية لي الأسطر التالية:

• مثال: log₃ (81)
  الإجابة: 4
• مثال: log₅ (125)
  الإجابة: 3

وحتى تتمكن من رسم الاقتران البياني f(x) =log₂ (x) يجب تعويض العديد من النقاط في الاقتران على الشكل التالي ويجب وضع النقاط على الرسم البياني والذي نصل بينهما بخط منحني وينتج من خلال ذلك الرسم الذي يوجد في الاسفل؛

• عند تعويض الرقم (1/4) سيكون الناتج هو -2. فتتكون النقطة (1/4، -2).
• عند تعويض الرقم (1/2) سيكون الناتج هو -1. فتتكون النقطة (1/2، -1).
• عند تعويض الرقم 1 سيكون الناتج هو 0. فتتكون النقطة (1، 0).
• عند تعويض الرقم 2 سيكون الناتج هو 1. فتتكون النقطة (2، 1).
• عند تعويض الرقم 4 سيكون الناتج هو 2. فتتكون النقطة (4، 2).

الدالة الجذرية

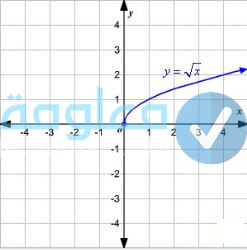
الاقتران الجذري هو من بين الاقترانات الحقيقية والتي يتم التعبير عنها من خلال الصيغة التالية: f(x) = √g(x). كما أن هذا الاقتران يتوفر على الكثير من الحدود. وحتى تتمكن من رسم هذا النوع من الاقترانات يجب تحديد مجال الاقتران ثم ايجاد بعض الصور لمجموعة من العناصر المجال ويتم تمثيلها في المستوى البياني، ثم يتم التوصيل بين النقاط من خلال خط منحني، وذلك لأن مجال هذا الإقتران يكون جميع الفيم التي تجعل ما تحت الجذر أكبر من او يساوي صفر. دعونا نتعرف في الأسطر التالية عن بعض الأمثلة توضح طريقة ايجاد المجال والرسم البياني الخاصة بهذا الاقتران.

مثال: f(x) = √x ، جد مجال الاقتران مع رسم المنحنى: 

للعثور على المجال يجب جعل ما تحت الجذر على شكل متباينة أبى او يساوي صفر على الشكل التالي:

x≥0 ، فيكون المجال هو { x: x ∈ R، x≥0} = [0 ، ∞)

ااٱن يمكن تعويض بعض القيم في الاقتران وذلك من أجل رسم الاقتران بالتمثيل البياني على المنحى الديكاتي د على الشكل التالي:

• عند تعويض الرقم 0 سيكون الناتج هو 0.
• عند تعويض الرقم 1 سيكون الناتج هو 1.
• عند تعويض الرقم 4 سيكون الناتج هو 2.
• عند تعويض الرقم 9 سيكون الناتج هو 3.

ليكون التمثيل البياني كما هو موضح في الصورة بالأسفل:

الدالة المتعددة (الاقتارن المتشعب)

الاقتران المتشعب وهو عبارة عن الاقتارن الذي يكون له أكثر من قاعدة واحدة ولما قاعدة مجال معين، فتتغير قاعدة المجال عند كل نقطة معين وتسمى هذه النقطة بنقاط التشعب. دعونا نقدم لكم في الاسفل صورة توضيحية عن الاقتران المتشعب.

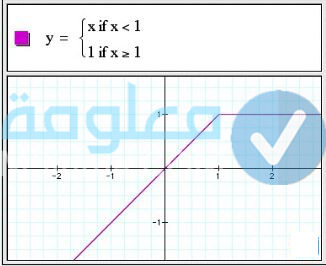
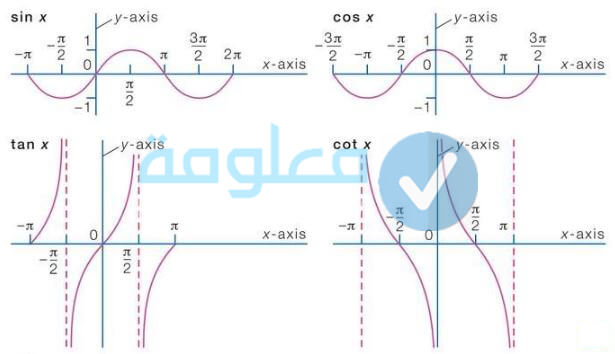
الدوال المثلثية في المثلثات القائمة الزاوية

تعتبر الاقترانات الدائرية من بين الاقترانات اللي تكرر نفسها والتي يطلق عليها بالإقترانات الدورية حيث تتضمن هذه الانواع من الاقترانات الجيب وجيب التمام والظل للمتغير (x) لتكون بالصور التالية:

• ((f(x) = sin (g(x
• ((f(x) = cos (g(x
• ((f(x) = tan(g(x

دعونا نتعرف على الرسم البياني الخاص بالدوال المثلثية:

قوانين الدوال المثلثية

توجد هناك العديد من القوانين التي تحكم الاقترانات الدائرية والتي تساعد في حال النهايات، والاشتقاق التفاضيلة وحل جميع المسائل التكامل، تم انشاء هذا لقوانين عند اشتقاقهها من خلال مجموعة من الطرق المعقدة، دعونا نتعرف على هذه القوانين من خلال الصور التالية والتي يطلق عليها المتطابقات المثلثية:

الدالة الزوجية والفردية

يوجد هناك نوعين من الدوال حسب تغير قيمة الاقتارن وذلك عند عكس إشارة المتغير الذي يتم تعويضه، وهذان النوعيه هما الدالة الزوجية والفردية، يتم التعبير عن الدالة الزوجية f(-x) = f(x)، بمعنى أن قيمة الاقتران لا تتغير عند تعويض القيمة x سواء كانت بقيمة سالبة او موجبة في مجال (x)f. أما الدالة الدالة الفردية هي التي تكون f(-x) = -f(x)؛ بمعنى تتغير القيمة الخاصة بها في حالة تعويض x بقيمة سالبة، حيث تكون القيمة الناتجة عكس قيمة الدالة الأصلية لجميع قيم x في مجال (x) f.

أمثلة عن دوال الفريدة:

دالة كثيرات الحدود والتي تكون مكونة من المتغير الأساسي فقط على سبيل المثال:

• f(x) = x⁵ ، f(x) = x³ ، f(x) = x ….
• دالة الجيب.
• دالة الظل (ظا).
• دالة ظل التمام (ظتا).
• دالة قاطع التمام (قتا).
• الدالة العكسية للجيب.
•  الدالة العكسية للظل.

أمثلة عن الدوال الزوجية:

• الدالة التربيعية والتي يكون فيها الاقتران مكون من المتغير الأساسي فقط مثل f(x) = x²
• دالة جيب التمام.
• دالة القاطع (قا).

خريطة مفاهيم تحليل الدوال

هناك مجموعة من الطلاب الذي يعتمدون على خرائط المفاهيم وذلك من أجل تسهيل فهم الأمور وحفظها، لهذا سنقدم لكم في هذه الفقرة من المقال صورة تمثل خريطة مفاهيم تحليل الدوال:

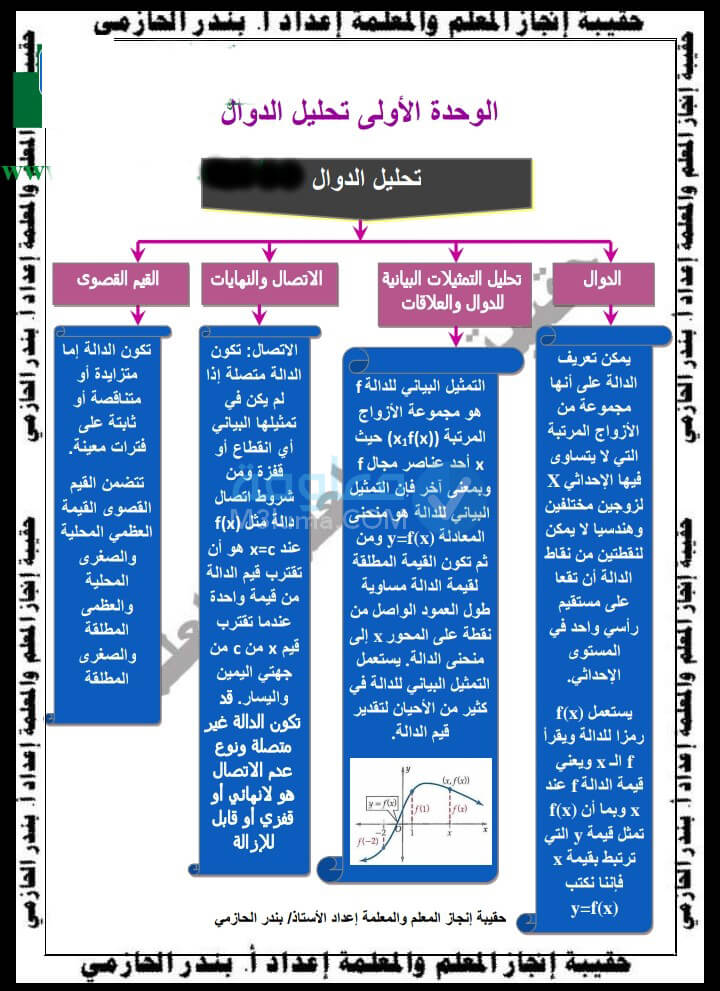
الدالة العكسية

الدالة العكسية هي من بين الدوال التي تمثل المعكوس الاقتران الاصلي والذي يرمز له لمعكوس الاقتران f(x) بالرمز f^-1(x)، يمكن أن نتأكد ما إذا كان معكوس الاقتران اقترانا أم لا، من خلال التأكد من جميع العناصر في المجال ترتبط بعنصر واحد في المدى (x)f نفسه، إذن هنا يكون الاقتران اقتران واحد لواحد، وذلك كما قلنا بعد التاكد من عناصر المجال وعناصر المدى، ومن خلال طريقة أخرى تسمى اختبار الخط الافقي وهي التي تمثل برسم خط افقي والتأكد من انه لا يقوم بقطع منحنى الاقتران في اكثر من نقطة واحدة.

في هذه الحالة يكون مجال الاقتارن (x)f هو مدة اقتران f^-1(x) ومدى الاقتران (x)f هو مجال الاقتران f^-1(x)، دعونا نتعرف في الأسطر التالية طريقة استخراج الاقتران العكسي من خلال المثال التالي تابعوا معنا الشرح:

مثال: f(x) = 4(x-5)

نقوم بكتابة الاقتران بصورة f(x) = y
اصبح لدينا الاقتران عل دى الشكل التالي: y = 4(x-5)

نجعل x موضوعا للقانون وذلك عن طريق الخطوات التالية:

• الاقتران الأصلي: y = 4(x-5)
  نضرب 4 بفرعي القوس فتصبح: y = 4x-20
  من خلال إضافة 20 إلى جانبي المعادلة فتصبح: y+20= 4x
  نقسم طرفي المعادلة على الرقم 4 فتصبح: y+20)/4= x)
• نبدل x ب y، ونبدل y ب x في صيغة المعادلة التي توصلنا إليها فتصبح:
  x+20)/4= y)
• نضع f^-1(x) مكان الرمز y فتصبح:
  x+20)/4=f^-1(x) )

الدوال الرئيسية الام والتحويلات الهندسية

هناك العديد من العمليات الأساسية التي تتمثل بها التحويلات الهندية التي يمكن إجرائها على الدوال، والتي من خلالها يتم تغيير من موقع الرسم البياني إلى الاقتران، وذلك عن طريق ارضافة رقم إلى الاقتران او رطح رقم منه او ضرب الاقتران برقم معين، أو عكس الاقتران يمكن ضربه برقم سالي على سبيل المثال. كما يمكن العثور على عملية التي تم اجرائها على الاقتران، عن طريق الرسم الأساسي والرسم الٱخر بعد اجراء تحويل، دعونا نقدم لكم صورة توضح التحويلات الهندسية الأساسية على الاقترانات:

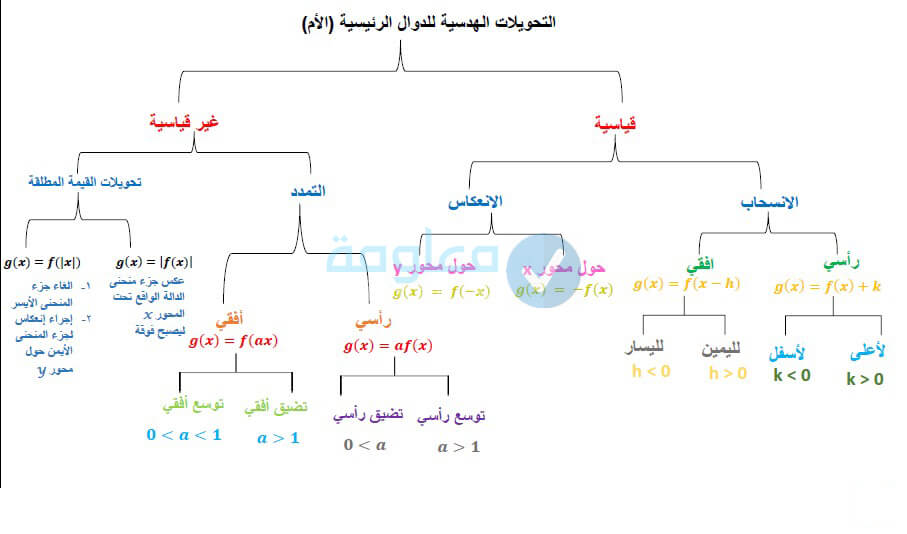
خلاصة

في النهاية كانت هذه جميع المعلومات المتعلقة بموضوع، بحث عن الدوال الحقيقية وأنواعها، شاركونا بتعليقاتكم أسفل المقال حول هذا الموضوع، وشكرا لكم على القراءة.