بحث عن المستقيمان والقاطع

بحث عن المستقيمان والقاطع
درس المستقيمان والقاطع أحد أكثر الدروس صعوبة في علم الرياضيات والجدير بالذكر أن هذا النوع من الهندسة هو الذي يسمى بالهندسة الإقليدية اي الهندسة المستوية، وهذه الهندسة هي نظام رياضياتي ينسب إلى إقليدس الألكسندرية وهي إحدى الأمثلة على الهندسة التركيبية التى تخص وصف خواص بسيطة متعلقة بالأجسام الهندسية كالنقاط والخطوط إلى مبرهنات عن تلك الأجسام دون إستخدام نظم إحداثية لوصفها، وهذا بالضبط عكس ما تعتمده الهندسة
التحليلية حيث توظف النظم لإحداثية في ترجمة المبرهنات الهندسية إلى صيغة جبرية.
وهذا الدرس، من الأبحاث التي يولى إليها الطلاب وخصوصا في الصفوف الأولى لتعلم مادة الرياضيات، فالنقاط والخطوط والزوايا تعد من ركائز الرياضيات وأساسياتها فمن خلالها نتمكن من تكوين مختلف الأشكال الهندسية.
وفي هذا المقال سنقدم بحثا عن المستقيمان والقاطع لتقديم كل المعلومات التي ستفيدك حول الموضوع فتابع معنا القراءة إذا كان يهمك الأمر.
بحث عن المستقيمان والقاطع
الخط المستقيم
الخط المستقيم هو شكل ذا بعد أحادي، ليس له عرض لكن له طول، ولكن ليس له سمك، يتكون من العديد من النقاط التي تمتد في اتجاهات متعاكسة إلى ما لا نهاية. أي أن المستقيم هو ذاك الخط الذي يصل بين عدد لا حصر له من النقاط، ومن الممكن رسمه من خلال توصيل كل نقطة بالأخرى. ونستطيع تحديد المستقيم وإعطائه إسما من خلال نقطتين خلال مستوى ثنائي الأبعاد. وبخصوص النقطتان اللتان توجدان على نفس
الخط تسميان نقطتان خطيتان. وفي الهندسة، هنالك أنواع متنوعة من المستقيمات كاالمستقيمات الأفقية، والمستقيمات العمودية، والمستقيمات المتوازية والمتعامدة.
القاطع
القاطع عبارة عن خط مستقيم يخترق شكلا هندسيا ما، مثلًا لو اخترق الخط المستقيم الدائرة من خلال تقاطعه مع نقطتين عليها، فهذا الخط المستقيم يسمى قاطعا بحيث أن القطعة المستقيمة الواقعة على الدائرة ستكون قطعا إما قطر في حال مرت بالمركز، أو وتر إن لم تمر به، أي أن القاطع يعد أحد حالة المستقيمات. ونحيطكم علما أن الفرق بين كل من المستقيم والقطعة المستقيمة، هو أن المستقيم ليس له بداية ولا حتى نهاية، أما القطعة المستقيمة فلها بدايية ولها نهاية أيضا .
أشكال المستقيمات
للمستقيمات عدة أشكال مختلفة لا تتشابه فيما بينها إذ أن لكل شكل منها تعريفه و ط
خصائصه ومن بين هذه الأشكال الكثيرة نذكر:
- °المستقيم: وهو ذاك الخط الذي يصل بينما لا نهاية من النقاط،لا يملك المستقيم بداية وأيضا ليس له نهاية، أي انه يمتد إلى المالانهاية من الجهتين.
- °القطعة المستقيمة: هوذاك الجزى من المستقيم الذي حددت لها نقطة بداية ونقطة نهاية أي أنه لم يعد مستقيما لأنه فقد إحدى خصائص المستقيم وأصبح له بداية ونهاية لكنه صار قطعة مستقيمية أي طرف من المستقيم.
- °الشعاع: هو جزء من مستقيم حددت لهه أي نقطة البداية ويمتد في اتجاه واحد فقط ويصل إلى ما لا نهاية.
أنواع الخطوط المستقيمة

تنقسم الخطوط المستقيمة إلى أنواع وهي كالتالي:
- °الخطوط البسيطة المستقيمة: يتم شرح الخطوط المستقيمة على أنها تلك الخطوط العادية بالرغم من اختلاف اتجاهاتها أو طريقة رسمها فهي تبقى خطوطا مستقيمية بسيطة حتى لو كانت مائلة أو رأسية أو أفقية أو متعامدة.
- °الخطوط غير المستقيمة البسيطة: هي الخطوط التي لا تفقد شكلها المستقيم وتصبح منعرجة مثل الأقواس والمنحنيات.
- °الخطوط المركبة: وهي تلك الخطوط التي ترتكز أساس في مكوناتها على خط مستقيم بسيط يمكن أن يكون في حالة انكسار أو تعامد أو توازي، ومن الممكن أيضا أن تكون تلك الخطوط مكونة بشكل أساسي من خطوط مركبة ومكونة من خط أساسي وخط أخر من الممكن أن يكون مستقيميا أو منعرجا هو أيضا.
الخطوط الافقية
تدل على الخطوط المرسومة التي يكون اتجاه المستقيم يبدأ من اليسار وينتهي الى اليمين في اتجاه واحد مستقيم دون إنحناء أو إنعراج، فهو يعد خطا أفقيا، وبمعنى آخر الخط الأفقي هو خط مستقيم يتم رسمه من اليسار إلى اليمين وهو مواز للمحور X في نظام إحداثيات المستوى. بطريقة آخرى ، يسمى الخط المستقيم عندما لا يقوم بأي تقاطع على المحور X ويمكن أن يكون له تقاطع على المحور Y يسمى الخط الأفقي. هذا يعني أن الخط الذي لا يلمس أي نقطة على المحور X من الممكن تسميته بالخط الأفقي.
الخطوط المتوازية
يمكن الإستعانة بهذا الإسم عندما لا يلتقي الخطان المستقيمان أو يتقاطعان في أي نقطة من نقاط المستقيم، أي منذ بدايته حتى اللانهاية، فيكونان متوازيان مع بعضهما البعض، يتم إسقط وتجسيد الخطوط المتوازية في الحياة الواقعية وفي الأشياء التي يقوم المرأ بصناعتها واختيارها فمن الممكن ان يرى المرء الخطوط الموازية لبعضها البعض في الحياة الواقعية أيضا إذا كان لدى المرء الصبر وقوة الملاحظة والتي تكون كافية للقيام بذلك. وكمثال لذالك، نجد خطوط السكك الحديدية. خطوط السكك الحديدية هي دائما ما تكون خطوطا متوازية حرفياً.
الخطان أو المساران لهما دور في مرور عجلات القطار للسفر على طول أي أنه لا يمكنك أن تسافر وشكل المساران منعرج. الفرق الكامن بين كل من الخطوط المتوازية التي تخيلها علماء الرياضيات وتلك التي يصنعونها المكلفون بمسارات السكك الحديدية، هو أن علماء الرياضيات لديهم الحرية في تخيل الخطوط المتوازية مرسومة على الأسطح المستوية والورق فقط ، بينما تسافر القطارات عبر جميع أنواع التضاريس ، من التلال والمنحدرات والجبال فوق الجسور, وفقًا لعلماء الرياضيات ، عندما نقوم برسم خطين متوازيين ، لابد أن يكون الخطين دائما في الزاوية نفسها ، مما يدل أنه سيكون لهما نفس المنحدر أو الانحدار.
الخطوط المتعامدة
نعني بالخطوط المتعامدة إلتقاء الخطان أو تقاطعاعهما بزاوية معينة كأن تكون 90 درجة أو يتقاطعان بزاوية قائمة، أي أنهما يكونان خطين متعامدين مع بعضهما البعض أي يقوم أحدهما بقطع أو فصل المستقيم إلى شقين.
الخطوط المتقاطعة
الخطوط المتقاطعة هي تلاقي خطين غير متوازيين عند نقطة معينة ونطلق على هذه الخطوط الخطوط المتقاطعة. والخطوط المتقاطعة عبارة عن سطرين يتشاركان في نقطة واحدة بالضبط. هذه النقطة المشتركة ما نسميه نقطة التقاطع.
الخط المستعرض
إن الخط المستعرض هو خط مستقيم يقوم بقطع خطين أو أكثر في بعض الحالات يكون متوازيا وفي حالات أخرى يكون غير متواز. الخط المستعرض غالبا ما يمر فوق أو عبر خطين في المستوى نفسه عند نقطتين متميزتين في مفهوم الهندسة. تملك المستعرضات دورا مهما في تحديد ما إذا كان خطان آخران في المستوى الإقليدي متوازيان أم لا.
معادلة الخط القاطع
بالضبط وكما تعلمنا من خلال الدرس الذي شرحنا سابقا، يقوم الخط القاطع بالتقاطع مع منحنى عند نقطتين أو أكثر. في الرياضيات ، عندما تكون لدينا نقطتين، نسميهما (x1 ، y1) و (x2 ، y2) ، في إمكاننا إيجاد ميل الخط المار بهذين النقطتين باستعمال الصيغة (y2 – y1) / (x2 – x1) . لا بذ من تذكر هذا ، ميل الخط هو معدل تغير y بالنسبة إلى x ، ومن هنا تم إقتباس الصيغة:
(التغير في y) / (التغيير في x) = (y2 – y1) / (x2 – x1)
بمجرد اكتشاف اميل الخط الذي يمر بهاتين النقطتين ، يصبح بإستطاعتنا حينها معرفة معادلة الخط المستقيم عبر هاتين النقطتين عن طريق إدخال إحدى النقطتين (x1 ، y1) والميل , تسمى هذه المعادلة بنقطة ميل الخط.
لذلك ، إذا إصبح في استطاعتنا إيجاد نقطتين على الخط القاطع ، فيمكننا وبكل سهولة إيجاد معادلة هذا الخط المستقيم دون عناء. وللقيام بذلك ، نقوم بإتباع الخطوات الأتية:
- •عليك أولا وقبل كل شيئ البحث وإيجاد نقطتين على الخط القاطع
- •في هاته الخطوة الثانية يجب عليك أن تجد ميل الخط الفاصل بين كل من النقطتين
- •قم بتعويض إحدى نقاط الميل في صيغة نقطة ميل الخط للحصول على معادلة الخط المستقيم.
تمارين على القاطع والمستقيم

سنقوم عزيزي القارئ بالحرص إيجاد تمارين تماما كالتمارين التي قد تواجهك في الامتحان على القاطع والمستقيم و المستقيمان المتقاطعان، أو الاسئلة التي يمكن ان تكون كالتالي:
من الممكن ان يطلب منك في التمرين أن ثبت أن المستقيمان غير متقاطعين؟، يمكنك الإستعانة بالبرهنة العكسية أي أن تقوم بإثبات أن المستقيمان المتوازيان وعندها نقول إذن المستقيمان غير متقاطعان ولا يمكن أن يتقاطعا.
من الممكن أيضا ان يكون التمرين علس شكل هذا السؤال ما وضعية أضلاع المثلث، في هذه الحالة تجدر الاشارة ان المثلث القائم دائما تكون أضلاعه المتلامسة متعامدة والاخر غير متوازيان، وفي الحالات الأخرى يكون كل مثلث به 3 أضلاع متقاطعة غير متعامدة ولا متوازية.
أما بالنسبة لامستطيل تكون أضلاعه متقابلة وكل اثنان متقابلان منهم متوازيان، والاخران متقاطعان مع المتوازيان كذلك الحال في المربع.
ما هي العلاقة بين المستقيمات والمستويات

تكمن العلاقة التي تجمع بين المستقيمات والمستويات هي مدى التوازي والتخالف بين المستقيمان المتوازيان، والمستقيمان المتخالفان.
فبخصوص المستقيمان المتوازيان فإنهما لا يتقاطعان بصلة نهائية ، كما نجدهم متواجدان في المستوى نفسه.
أما بالنسبة للمستقيمان المتخالفان فهما مستقيمين ليس من الممكن أن يتقاطعا، بالإضافة إلى أنه لا يمكن أن نجدهم يقعان في ذات المستوى.
ومن المهم تذكر أن المستويان المتوازيان هما نفسهما المستويان الغير متقاطعين.
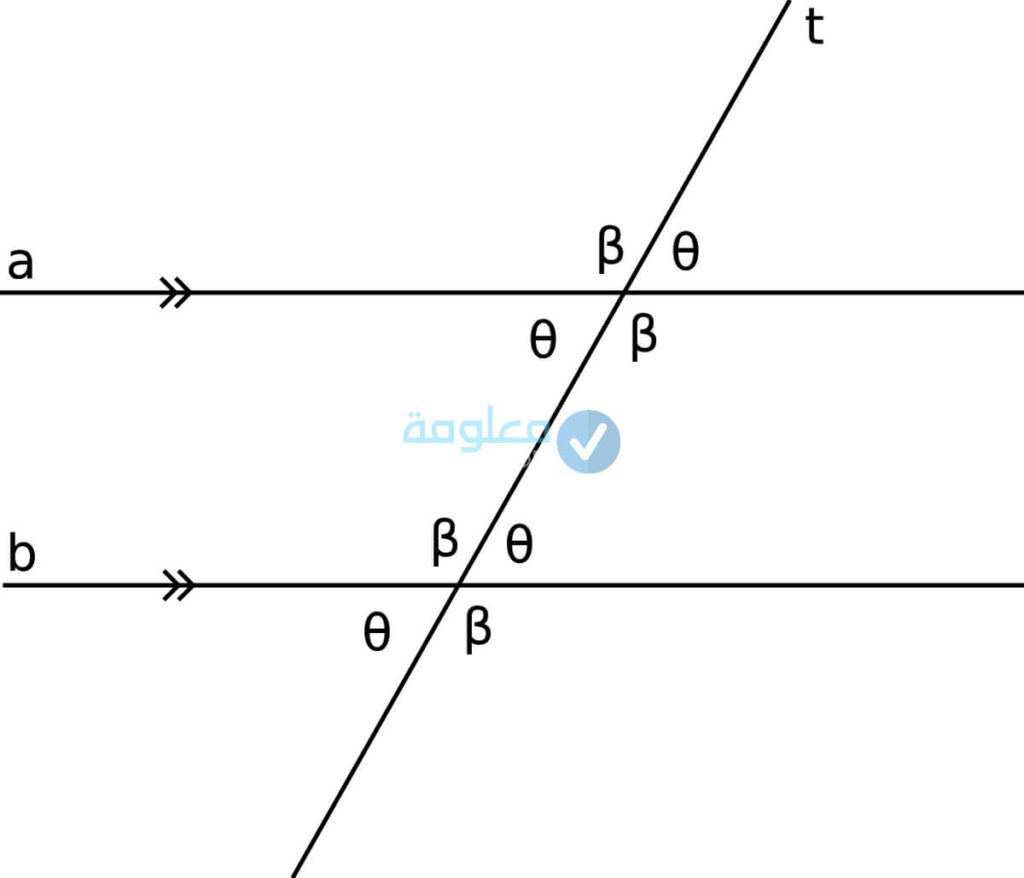
أما بإنتقالنا للتحدث عن الزوايا، أن الزوايا التي يتم تشكيلها في هذه التقاطعات هي التي تسمى المتطابقات، إذ أن المستقيمان a,b المتوازيان والمستقيم القاطع هو الذي نرمز له t.
الزوايا والمستقيمات

تعرف الزاوية على انها عبارة عن الشكل الذي ينتج عن تلاقي أما شعاعين أو مستقيمين في نقطة واحدة، ويشكل هذان المستقيمان الإثنان الأضلع الخاصة بالزاوية، وتسمى نقطة التقائهما رأس الزاوية، وتكثر أنواع الزوايا التي تنتج عن وجود تقاطع بين مستقيمين:
- °الزوايا الداخلية
هي تلك الزوايا التي تنتج عن التقاطع بين المستقيمين.
- °الزوايا الخارجية
تدل عليها تلك الزوايا التي تكوه في الجهة الخارجية من المستقيمين.
- °الزاويتان المتحالفتان
هما زاويتان اثنتين داخلتين في نفس الجهة من القاطع الذي يقوم بقطع المستقيمين المتوازيين.
- °الزاويتان المتبادلتين داخلياً
هما الزاويتان الداخلتين اللتان لا تنتميان لنفس الجهة وليستا متجاورتين، أي أن كل منهما تقع في جهة خاصة بها
- °الزاويتان المتبادلتان خارجياً
هما زاويتان متبادلتان، تتشكلان بطريقة غير متجاورتين اي ان كل واحدة في جهة مختلفة من القاطع.
- °الزاويتان المتناظرتان
هما الزاويتان المتشكلاتان في جهة واحدة فقط من القاطع وفي الاتجاه نفسه للمستقيمين.
نظريات المستقيمات والزوايا

توجد العديد من النظريات في الرياضيات والتي كان الدور من إقامتها تحديد العلاقة بين كل من المستقيمات والزوايا وهي:
- °نظرية القاطع العمودي: تدل هذه النظرية على أنه عندما يكون هناك مستقيمين متوازيين ويتعامد مستقيم على أحدهما، فهو بالتالي يصير متعامدا أيضا على المستقيم الثاني.
- °نظريات المستقيمان المتوازيان وازدواج الزوايا: تدل هذه النظرية على تنص على وجود 8 زوايا نتيجة قطع مستقيمين، ما بين الزوايا المتحالفة والزوايا المتبادلة خارجيًا والمتبادلة داخليًا.
- °نظرية مسلمة الزاويتين المتناظرتين: ومعنى تلك النظرية على أنه إذا كان هناك قاطع وقام قطع مستقيمين متوازيين، تصبح كل زاوية من زاويتي المستقيمين متماثلة ومتناظرة مع الأخرى التي سبق وتم رسمها.
شكرك عزيز القارئ على قراءة محتوانا حول المستقيمان والقاطع، نتمنى أن تكون قد إستفدت من خلال مقالنا هذا فإذا كنت طالبا فهنيئا لك لأنك اخترت الصفحة التي جمعت كل المعرف بعناية لتقدمها لك بالتدقيق وبالتفصيل الممل لمساعدتك على تحصيل العلومات وتبسط كل ما هو صعب عليك.










